• Eine diskrete Zufallsvariable \(X\), die die Anzahl der täglichen S-Bahn Ausfälle misst, ist poissonverteilt mit Ausfallrate \(\lambda > 0\); in Formelzeichen: \(X \sim \text{Pois}(\lambda)\). Hierbei wird vorausgesetzt, dass die S-Bahnen eine konstante Ausfallrate haben.
• Eine poissonverteilte Zufallsvariable hat die diskrete Dichte / Wahrscheinlichkeitsfunktion
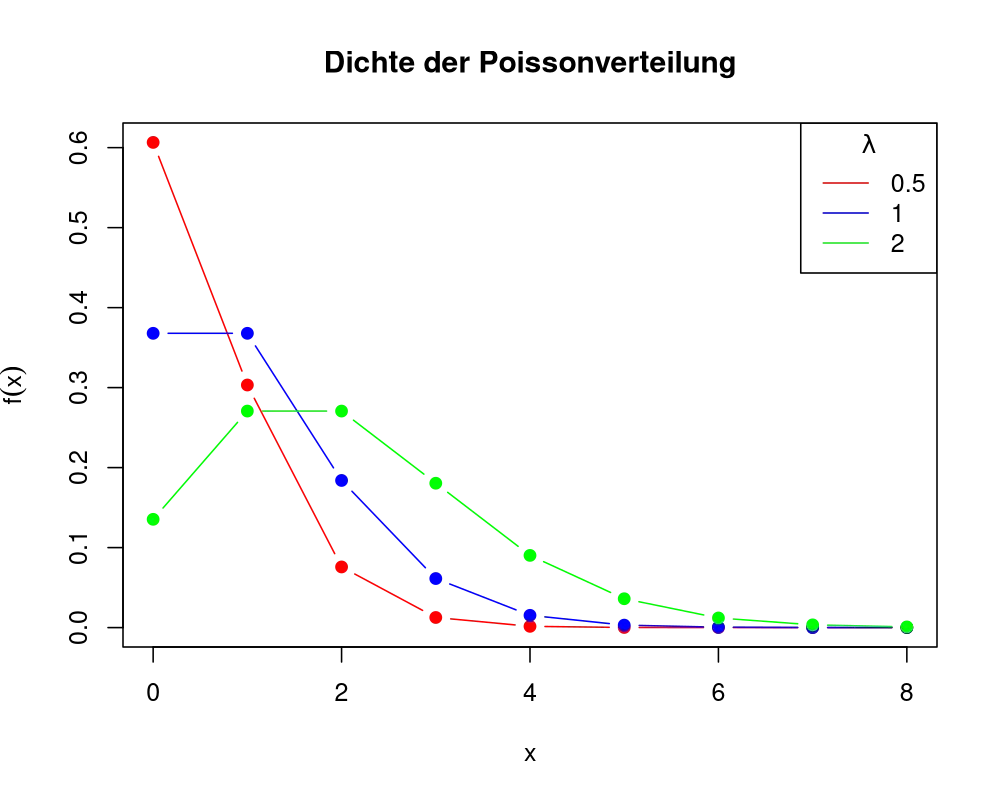
  \(f(x) = P(X = x) = \frac{\lambda^x \exp(-\lambda)}{x!}\mathbb{I}_{\mathbb{N}_0}(x)\)
  Hierbei bezeichnet \(\mathbb{N}_0 = {0, 1 , 2, \ldots} \; \text{und} \; x! = 1\times 2 \times \ldots \times (x - 1) \times x\)
• Die Verteilungsfunktion \(F(x)\) berechnet sich zu:
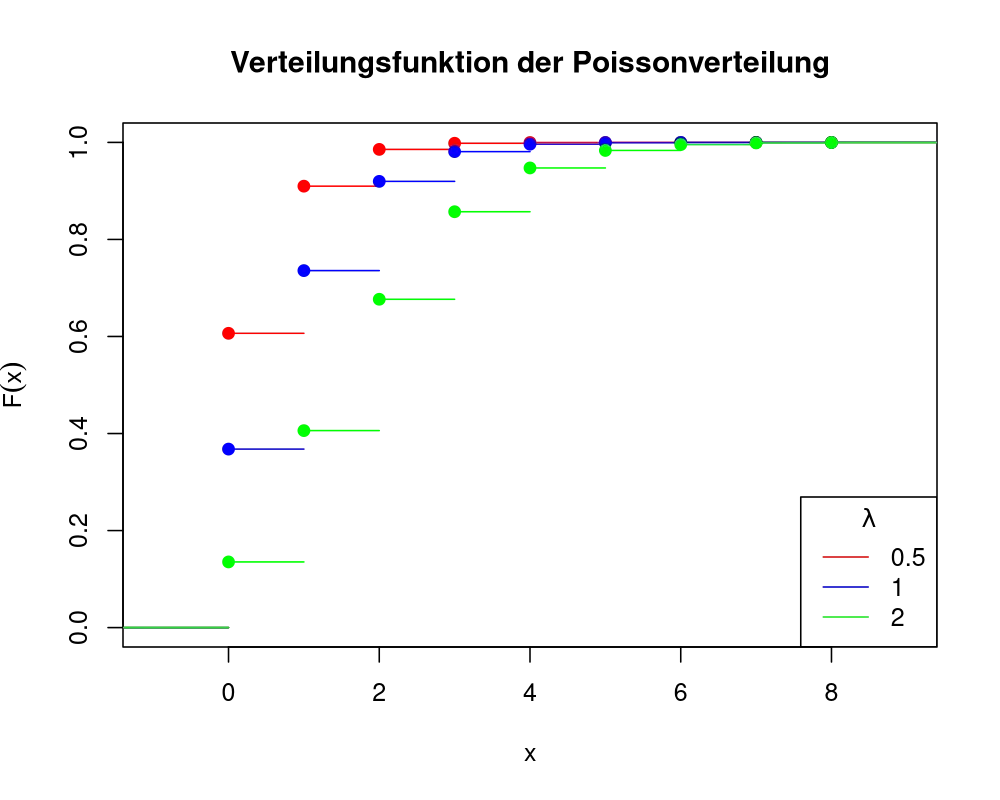
  \(F(x) = \sum_{i = 0}^{\lfloor x \rfloor} \frac{\lambda^i \exp(-\lambda)}{i!}\), wobei \(\lfloor x \rfloor\) \(x\) auf die nächst kleinere natürliche Zahl abrundet.
• Die Quantilsfunktion \(F^{-1}(q) = x\) ermittelt sich aus der Verteilungsfunktion
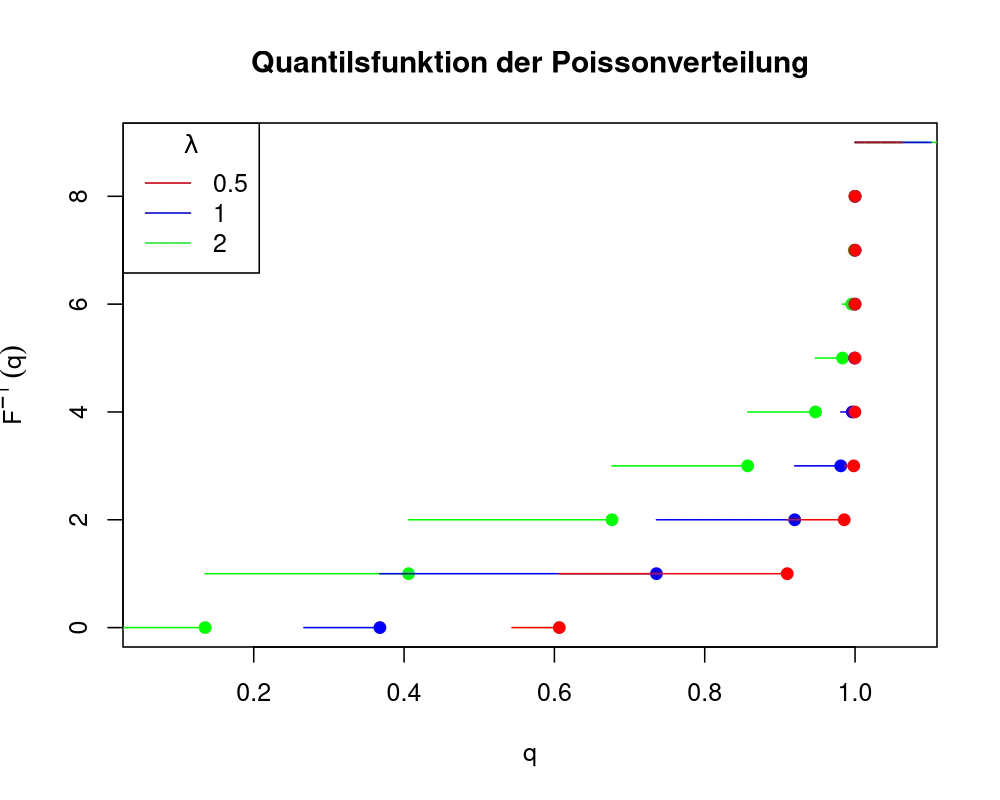
  \(F^{-1}(q) = \inf \{x \in \mathbb{R}: F(x) \geq q \} \)
  
• Der Erwartungswert ist:
  \(\mathbb{E}(X) = \sum_{x = 0}^{\infty} x \frac{\lambda^x \exp(-\lambda)}{x!} = \sum_{x = 1}^{\infty} x \frac{\lambda^x \exp(-\lambda)}{x!} = \sum_{x = 1}^{\infty} \frac{x \lambda^x \exp(-\lambda)}{x ( x- 1)!} = \) \(\exp(-\lambda) \lambda \sum_{x = 1}^{\infty} \frac{\lambda^{x - 1}}{(x - 1)!} = \exp(-\lambda) \lambda \sum_{x = 0}^{\infty} \frac{\lambda^{x}}{x!} \)
  • Definition der Exponentialfunktion: \(e^x = \exp(x) = \sum_{i = 0}^{\infty} \frac{x^i}{i!}\)
  \(\Rightarrow \mathbb{E}(X) = \exp(-\lambda) \lambda \exp(\lambda) = \lambda \exp(-\lambda + \lambda) = \lambda \)
• Die Varianz berechnet sich durch \(\mathbb{E}(X) = \mathbb{E}(X^2) - (\mathbb{E}(X))^2\):
  \(\mathbb{E}(X^2) = \sum_{x = 0}^{\infty} x^2 \frac{\lambda^x \exp(-\lambda)}{x!} = \sum_{x = 0}^{\infty} \frac{x^2 \lambda^x \exp(-\lambda)}{x (x - 1)!} = \exp(-\lambda) \lambda \sum_{x = 1}^{\infty} \frac{x \lambda^{x - 1}}{(x - 1)!} = \) \(\exp(-\lambda) \lambda \left[ \sum_{x = 1}^{\infty} \frac{x - 1}{(x - 1)!} \lambda^{x - 1} + \sum_{x = 1}^{\infty} \frac{1}{(x - 1)!} \lambda^{x - 1}\right] = \) \(\exp(-\lambda) \lambda \left[ \sum_{x = 2}^{\infty} \frac{x - 1}{(x - 1)(x - 2)!} \lambda^{x - 1} + \sum_{x = 0}^{\infty} \frac{1}{x!} \lambda^x \right] = \) \(\exp(-\lambda) \lambda \left[ \sum_{x = 2}^{\infty} \frac{\lambda^{x - 1}}{(x - 2)!} + \exp(\lambda) \right]\) \(\exp(-\lambda) \lambda \left[ \lambda \sum_{x = 2}^{\infty} \frac{\lambda^{x - 2}}{(x - 2)!} + \exp(\lambda) \right] = \exp(-\lambda) \lambda \left[\lambda \exp(\lambda) + \exp(\lambda)\right] = \) \(\lambda^2 + \lambda \Rightarrow \text{Var}(X) = \lambda^2 + \lambda - \lambda^2 = \lambda\)