• Eine stetige Zufallsvariable \(X\), die die Zeit zwischen zwei S-Bahn Ausfällen misst, ist exponentialverteilt mit Ausfallrate \(\frac{1}{\lambda}, ~ \lambda > 0\); in Formelzeichen \(X \sim \text{Exp}(\lambda)\). Hierbei wird vorausgesetzt, dass die S-Bahnen eine konstante Ausfallrate haben.
• Eine exponentialverteilte Zufallsvariable hat die stetige Dichte \(f(x) = \lambda \exp(-\lambda x) \mathbb{I}_{[0, \infty)}(x)\)
  
• Die Verteilungsfunktion \(F(x)\) berechnet sich zu:
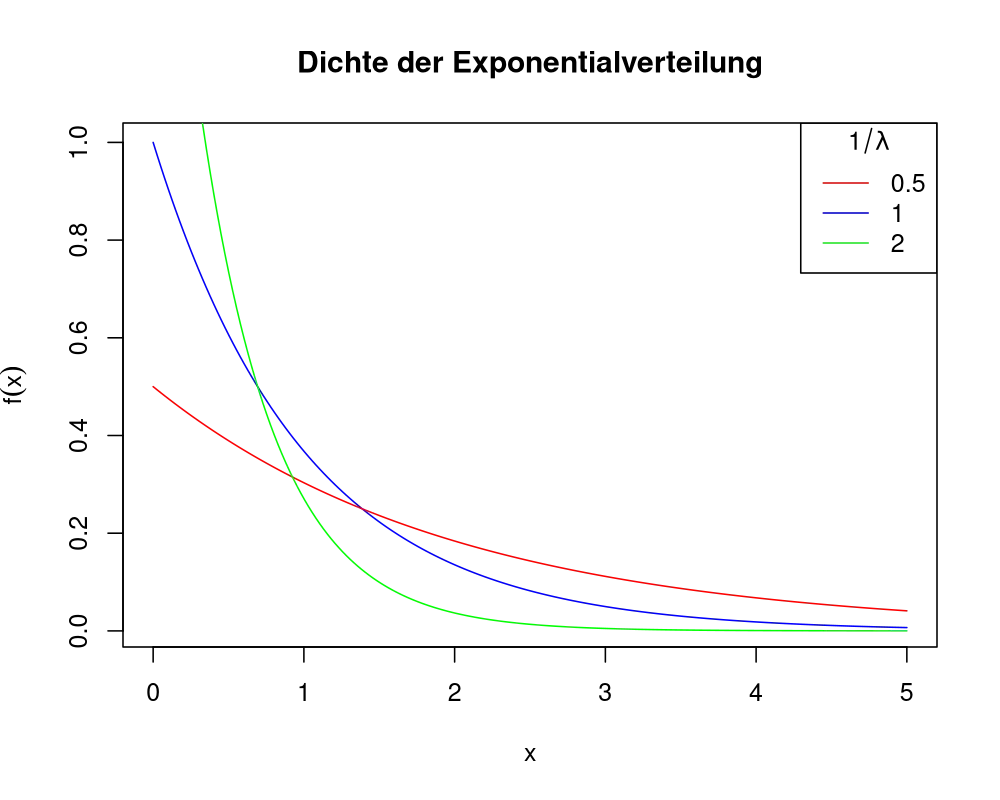
  \(F(x) = \int_{-\infty}^x f(z) dz = \int_{0}^x \lambda \exp(-\lambda ~ z) dz = \lambda \int_{0}^x \exp(-\lambda ~ z) dz = \)
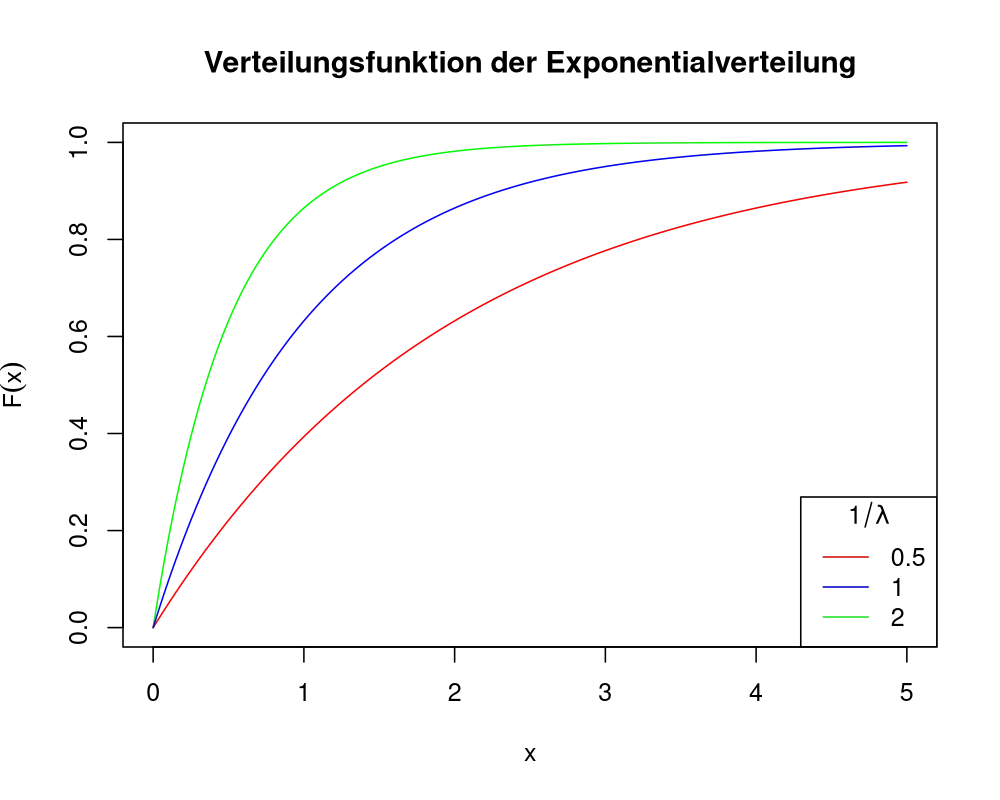
  \(\lambda \left[-\frac{1}{\lambda} \exp(-\lambda z)\right]^{z = x}_{z = 0} = \lambda\left[-\frac{1}{\lambda} \exp(-\lambda x) + \frac{1}{\lambda} \exp(-\lambda 0) \right] = 1 - \exp(-\lambda x)\)
  
• Die Quantilsfunktion \(F^{-1}(q) = x\) ermittelt sich aus der Verteilungsfunktion
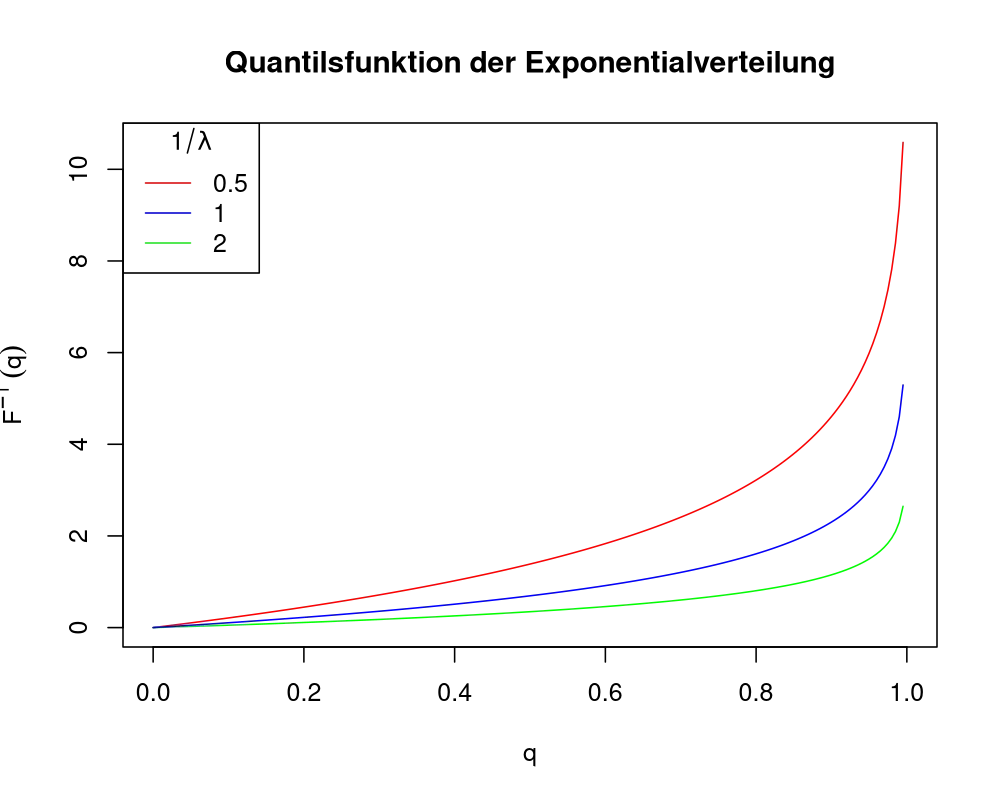
  \(q = 1 - \exp(-\lambda x) \Leftrightarrow 1 - q = \exp(-\lambda x) \Leftrightarrow \ln(1 - q) = -\lambda x \) \(F^{-1}(q) = -\frac{\ln(1 - q)}{\lambda} \)
  
• Der Erwartungswert ist:
  \(\mathbb{E}(X) = \int_{-\infty}^{\infty} zf(z) dz = \int_0^{\infty} z \lambda \exp(-\lambda ~ z) dz = \lambda \int_0^{\infty} z \exp(-\lambda ~ z) dz =\) \(\lambda \left[ -z \frac{1}{\lambda} \exp(-\lambda z)\right]_{z = 0}^{z \rightarrow \infty} - \lambda \int_0^{\infty} -\frac{1}{\lambda} \exp(-\lambda z) dz = \left[-z \exp(-\lambda z) \right]_{z = 0}^{z \rightarrow \infty} + \left[\frac{1}{\lambda}\exp(-\lambda z)\right]_{z = 0}^{z \rightarrow \infty}\)
  • Berechnung von \(\lim_{z \rightarrow \infty} z \exp(-\lambda z)\) mit der Regel von L'Hôpital:
    Voraussetzung: \(\lim_{z \rightarrow \infty} z = \lim_{z \rightarrow \infty} \exp(\lambda z) = \infty \)
    Anwendung: \(\lim_{z \rightarrow \infty} z \exp(-\lambda z) = \lim_{z \rightarrow \infty} \frac{1}{\lambda \exp(\lambda x)} = 0 \)
  \(\Rightarrow 0 + \frac{1}{\lambda} = \frac{1}{\lambda} \)
• Die Varianz berechnet sich durch \(\mathbb{E}(X) = \mathbb{E}(X^2) - (\mathbb{E}(X))^2\):
  \(\mathbb{E}(X^2) = \int_{-\infty}^{\infty} z^2 f(z) dz = \int_0^{\infty} z^2 \lambda \exp(-\lambda z) dz = \lambda \int_0^{\infty} z^2 \exp(-\lambda z) dz = \) \(\lambda \left[-z^2 \frac{1}{\lambda} \exp(-\lambda z)\right]_{z = 0}^{z \rightarrow \infty} + \lambda \int_0^{\infty} 2z \frac{1}{\lambda} \exp(-\lambda z) dz = \left[-z^2 \exp(-\lambda z)\right]_{z = 0}^{z \rightarrow \infty} + 2 \frac{1}{\lambda}\mathbb{E}(X) = \)
  • Berechnung von \(\lim_{z \rightarrow \infty} z^2 \exp(-\lambda z)\) analog zu oben:
    Voraussetzung: \(\lim_{z \rightarrow \infty} z^2 = \lim_{z \rightarrow \infty} \exp(\lambda z) = \infty \)
    Anwendung: \(\lim_{z \rightarrow \infty} z^2 \exp(-\lambda z) = \lim_{z \rightarrow \infty} \frac{2z}{\lambda \exp(\lambda x)} = 0 \)
  \(\Rightarrow 0 + \frac{2}{\lambda^2} \Rightarrow \text{Var}(X) = \frac{2}{\lambda^2} - \frac{1}{\lambda^2} = \frac{1}{\lambda^2}\)